______________________________________

My story of learning involves both my story as well as that of my students. The teaching of mathematics should be the teaching of ideas Mathematics is the ideal content vehicle through which to teach thinking, the thinking that comes through being cognitively challenged. This is about my journey whilst teaching  mathematics over many years. It’s about how I have come to believe things about ideal classroom practice. It’s about reflecting on practice and negotiating change. Ultimately it’s about learning. Mine and my students. And that of current and future educators of mathematics.

______________________________________

“There is no story, no set of events that leads anywhere or proves anything - no middle, no end. Just a glimpse through a half-open door, voices seen not heard, vibrations sensed through a wall while the trained ear strains, not to hear what is passing in the next room, but to measure the chords....and the voice that names them your own”

What follows is a glimpse into my thinking, and my practice, and how these have possibly influenced my students’ thinking in mathematics. It is my voice, or, at the very least, its echo, yet I start by paying tribute to the many educators who have helped shaped this voice. We all live in the shadow of others.

I hope that the reader’s ‘trained ear’ picks up something of interest, recognises the subjectivity of this account and measures its effects accordingly.

I am conscious that any 'story of learning' is one that involves students’ learning as well as my own. In every story of learning is an associated, sometimes parallel, story of practice.

So, where to start?

Mathematics is all about reason. It’s about ideas. There is a poem by Peter Hooper which is partly given below:

Poetry isn’t in my words

It’s in the direction I’m pointing

If you can’t understand that

And if you’re appalled at the journey

Stick to the guided tours

Perhaps teaching and learning are much like this – the journey is the real education; the content merely the means by which we explore the landscape. How do we create a landscape worth exploring? How do we interact with it, how do we traverse it? How do we point in the right direction?

Do we sometimes forget about the journey in our desire to get to the destination? (Which is what?)

My strongly held belief is that the teaching of ideas should be the determining paradigm in the teaching of mathematics. These big ideas are the peaks of the landscape, the things we look out upon, appreciate for their beauty and use to guide our journey. Looking at, and placing, where we put our feet are the skills of the discipline. The metaphor can be extended. One can scale the peaks by following in the footsteps of another, having porters doing the heavy lifting and carrying and setting up camp where others decide. The journey isn’t easy even with all of this. Take away the porters, take away the leaders, take away the determined paths and put that same person in an unfamiliar landscape. Have they learnt anything from their previous experience that allows them the opportunity to undertake another journey, independently? Is that important?

“What you have been obliged to discover by yourself leaves a path in your mind which you can use again when the need arises.”    –G. C. Lichtenberg

I used to think that my primary aim, as a teacher of mathematics, was to translate the ideas into ‘user-friendly’ chunks for students, use clear and well-explained examples, source interesting and fun activities and help students come to their own understanding by asking leading questions without directly ‘telling’ students what to do when they became ‘stuck’. Malcolm Swan calls this approach to the teaching of mathematics the XXX model - Xplanation Xample, Xercise.

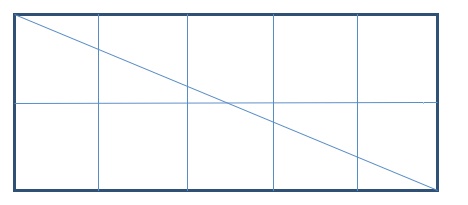
In the 1980s, problem solving became a focus in the teaching of mathematics and a light bulb came on in my head. Thinking became the goal. All I had to do was to teach ‘problem solving’ and everything would be fine; the rest would follow. I remember designating every Friday problem solving, including for instance the problem below.

Problem: How many tiles does this diagonal go through? Is there a pattern relating this to the size of the rectangle? Investigate.

A collection of such problems exemplified various strategies such as: careful reading, making lists, working systematically, looking at a simpler case, looking for patterns, using educated trial and error. Students seemed to enjoy these problems and I felt I was making a difference, improving their thinking.

Yet...

Whilst the teaching of thinking via problem solving was seen as important, and problem solving became a part of assessment tasks, it didn’t really change the way teachers approached the ‘main game’ of instruction in the curriculum content, nor the big ticket assessment tasks such as tests. If it was part of a course or test, it was an unrelated activity that was labelled ‘extension’ or a ‘fun question’ at the end of the test. And we show what we value through what we assess.

During the 1990s, I was fortunate to be introduced to the work and thinking of Dr Julia Atkin. In one of her papers she put forward a question that I have modified, and expanded upon, for my own purposes:

Instead of asking the question “What topics do we need to cover?” we need to aim to develop processes and approaches which result from asking “What are the powerful ideas and processes that we believe are important for young people to learn in mathematics?”

Our goal is then to develop syllabi around desired understandings – the big ideas – then ask “What information and what experiences do we engage the students in, in order for them to develop these understandings?”

The focus of assessment is in terms of the further question “If students understand this idea, how can they demonstrate it?”

This was my next light bulb moment. The task of the teacher is not to put knowledge where it does not exist, but rather lead the mind’s eye so that it might see for itself. Our goal as teachers should be to provide learning opportunities within the curriculum that develop the students’ capacity to construct their own understandings and deliberately plan lessons that offer, support and develop rich and authentic thinking. Students learn best when constructing their own knowledge. This is not, however, to imply teachers are ‘merely’ guides on the side or ‘facilitators’ (horrible word). Teachers do important work. To ensure that we teach for understanding, teachers need to deliberately plan for learning to occur, for meaning to be made and for transfer across contexts to be engendered. This requires hard, reflective effort. Curricula need to target the understandings we want to elicit and focus our activities in class on developing those understandings in ways that compel students to form the cognitive structures and pathways that lead to mathematical learning.

Teaching for understanding involves thinking – deep, sustained thinking that leads to students being able to construct an abstraction in their minds that makes sense of many distinct pieces of knowledge. This thinking should be done by both teacher and students.

Over the last ten years or so I have come to believe that, in order to engender this thinking in students, teachers also need to engage in ‘rich and authentic thinking’ about what we do and why; that purposeful teaching should be the paradigm of education. It’s a case of being more mindful. Education is too important to leave to chance.

The goal is now to purposefully design learning activities, not ‘just’ for their entertainment value and interest factor, but to engender the thinking that develops an understanding of the big ideas of the discipline and develop, support and encourage learning approaches so that students can authentically ‘do mathematics’.

Research has shown that students who solve difficult problems on their own — without the help of other students or teachers — often gain a better understanding of mathematics concepts. The learning comes with the struggle. I think I’ve always believed this, but struggled myself, to articulate my reasons for holding such a belief. Yet another light bulb moment came as I listened, and read about, how neuroscience is enriching and developing our ideas about learning and what occurs in the brain as we learn.

At the Australian Council for Educational Leaders (ACEL) conference in Melbourne in 2008, Martin Westwell from Flinders University spoke on learning and what neuroscience says about learning. He argued that the way our brains are ‘wired up’ depends on the number and type of connections made. These connections are determined by our experiences. These lines of communication between brain cells consequently determine the learning formed. It is the interconnectivity of ideas between cells that transforms information into learning. Repetition of these experiences re-inforces the connections. It is important, therefore, to ensure the connections are those that produce quality thinking rather than regurgitating a learnt script. It isn’t important how the information gets into the brain but what the brain does with it when it receives it.

Anxiety (especially long term), just like how we are educated, changes the way we think…there is an emotional component. Anxiety can physiologically prevent us from achieving our potential; it inhibits learning. This made me think about intervening to improve learning; intervening when affective learning behaviours are not going to produce optimal learning as well as intervening when cognitive behaviours aren’t conducive.

Martin mentioned an experiment done with a group of young African-American boys in the US, who were given an IQ test. Half were just given the questions. The other half were first asked to tick a box to describe their ethnicity. Even though the groups’ ability make-up was very similar, the second group produced significantly fewer IQ points than the other. Just the act of having to state their ethnicity was enough to stir up thoughts of societal expectations and depress their performance. Students who think of their intelligence as fixed usually have achievements that decrease over the course of their schooling. Those who believe intelligence is malleable are more resilient, can come back from failure, don’t give up as easily, and show a positive trajectory in terms of their achievements.

The executive functions of the brain that we should be encouraging and promoting in the way we teach are:

·        Concentration

·        Resisting temptation

·        Delayed gratification

·        Self-directed/interdependent learning

·        Problem solving

·        Creativity/Innovation

The environment we create in classes and schools can affect how students develop their intelligence. Take, for example, the experiment done with mice which were deliberately injected with Huntington’s Disease, a disease that withers the brain. Huntington’s is a genetically inherited disease. If you have the gene, you develop it…or do you? Only 20% of the infected mice who were placed in a rich environment full of wheels, crawl tunnels etc actually developed the disease. 100% of the infected mice, who were placed in an environment in which no stimuli were provided, developed the disease.

These stories affected me deeply. I was responsible for providing a rich environment in my classes to support the development of quality thinking. I was responsible for ensuring students believed that they had the power to change their performance and that their performance level wasn’t immutable. How was I to do this?

I came to the conclusion that the way to go was to identify students’ prior learning, devise associated, targeted intervention to address any misconceptions or misunderstandings, and then examine instruction that  would move learning forward for each student.

In mathematics, intervention has sometimes been left too late for this to be effective. Neuroscience tells us that neural networks can be created that contain strong, yet incorrect, thinking pathways due to incomplete understanding or misrepresented patterns. It isn't good enough to form new networks with the same knowledge as students will 'revert' to the bedded down networks when under stress (eg in tests). The better way is to directly address the incorrect connections and 'fix' them.

For example, a history teacher noticed that every year her students confused Martin Luther the philosopher with Martin Luther King. Saying "Martin Luther is not the same person as Martin Luther King" didn't help - the association in the same sentence just re-inforced the connection in students' brains. Just informing students about Martin Luther didn't help. When she deliberately addressed the incorrect connection by asking "Why do you think Mr and Mrs King named their child after Martin Luther?" there was finally some success. She had identified the misconception in their thinking and deliberately addressed it to change that connection. This then was re-inforced to strengthen it.

This is what I wanted to do in mathematics:  to try and devise learning activities that avoid these incorrect pathways being formed in the first place with new knowledge (and to what extent is any knowledge 'new' one may ask) and, simultaneously, to devise ways of eliciting the misconceptions that students may have formed previously and deliberately address these so that the incorrect thinking pathways are replaced by more effective ones. All this within a classroom context that rewards and supports academic risk-taking and develops within students a self-belief that performance change is possible…

Whilst thinking about the ways in which I could achieve this, I re-visited the Gradual Release of Responsibility framework for classroom learning, which outlines a path of progression from teacher- to student-centred learning. It has four components:

1. 1.The first involves the teacher in articulating and modelling the purpose of the lesson, using the type of thinking and language needed for it.
   

2. 2.The second component is guided instruction: the teacher applies questions and prompts that gradually encourage students to assume responsibility for their own learning. The questioning may be addressed to the whole class but is more often used for smaller groups with similar learning needs.
   

3. 3.The productive group work component involves students in collaboration around a task related to the central topic. The students are expected to use suitable academic language and are individually accountable for their efforts.
   

4. 4.The final component is independent learning, in which each student applies what they have learnt within or outside the class.
   

Two diagrammatic views of this framework are given below:

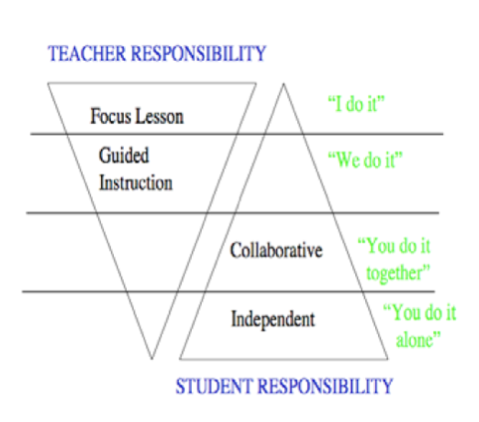
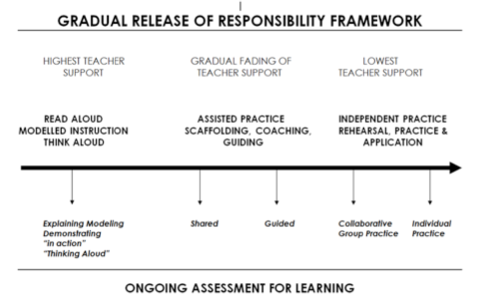
I have tried to use more of the ‘questions and prompts for mathematical thinking’ at Stage 2 of the above framework in my instructional practice.

I’ve always liked the Socratic nature of teaching through planned questions that ‘ratchet up’ the thinking as the lesson progresses. You can start with questions that determine ‘entry level’ and those that address misconceptions then prompt students to interconnect and interweave their constructed meanings with new knowledge.

However, whilst the learning can be ‘scaffolded’ by purposeful use of questions by teachers, there must also be ‘fading’ or the engagement in the learning never moves from the teacher’s brain to the student’s. Teachers need to know when to intervene and when to ‘fade out’. If students don’t learn to ask themselves the ‘right’ questions to get them going on an unfamiliar and challenging learning task then we have failed as educators. As John Mason says, ‘students are likely to remain dependent on the teacher asking certain questions. Thus they are only being trained in dependency’. To try and ‘train’ students to ask what I consider to be the right questions that increase their chances of being more independent and self-sufficient learners, I have tried to use instructional practices that decrease dependence on me. I have also used self-reflective tools to focus students’ attention on their innate ability to help themselves.

In a presentation at the University of Melbourne in 2009, Malcolm Swan gave a list of instructional strategies that engender a collaborative learning/intellectual challenging mathematics classroom:

*network of ideas

*social activity/discourse

*students are challenged through prompting-thinking questions that offer cognitive dissonance

*recognition of misunderstandings, making these explicit and learning from them (effective feedback)

He suggested some thinking-prompt questions that could engender great student discourse and also elicit some misconceptions for the teacher to work with. For example: Hand out numbers on cards to groups of students (eg. square root of 2, four-fifths, cube root of 8, negative 7) and ask students to write down everything you know about, or can find out about, this number.

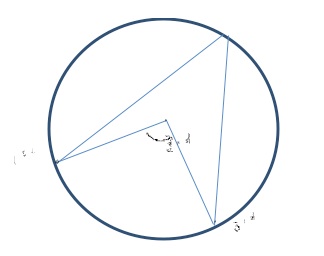
I have tried this approach with Y10 circle geometry. I gave students some diagrams (example below) and, with the help of a software program called CABRI GEOMETRE, they were to construct the diagrams and find out everything they could about them.

I gave them minimal information about using the program. Questions such as “How do I get the program to measure this angle?” were met with other questions such as “Hmmm...well...let’s think. What makes the angle in the first place?” In this way, even though I had to go through this conversation a number of times, students were forced to think about an angle being an amount of turning between two ‘arms’ around a pivotal point. The program measured angles identified by the user clicking on the three key points in turn that defined the angle. (Shown above). Whilst not being just ‘told’ straight away how to do this, caused frustration for some students, they did learn about angles as well as discovering for themselves how to perform this operation.

John Mason, in his book, Questions and Prompts for Mathematical Thinking, gives examples of questions to illustrate the six overarching aspects of mathematical thinking:

1.Exemplifying and Specialising

2.Completing, Deleting and Correcting

3.Comparing, Sorting an Organising

4.Changing, Varying, Reversing and Altering

5.Generalising and Conjecturing

6.Explaining, Justifying, Verifying, Convincing and Refuting

Examples include:

For Completing, Deleting and Correcting

•To Use a Definition

For example: Which statements can be deleted? A rectangle has four right angles, at least three right angles, at least two right angles, at least one right angle, two pairs of parallel sides, at least one pair of parallel sides, two pairs of opposite sides equal, diagonals that bisect, interior angle sum of 360 degrees.

Students are being challenged here to think about what is absolutely necessary to define a rectangle and what is superfluous. What can be deduced from the absolute?

•To Use an Example/Counter-Example:

For example: What can be done when some students always dominate and some end up being more firmly bound to their lack of thinking as they just sit back and wait for others to do the thinking for them? At times group work in mathematics does not add value to students’ thinking but becomes detrimental as the challenge and feeling of being ‘stuck’ is merely confirmed.

I have been most fortunate to work with Ron Ritchhart of Project Zero at Harvard University over the last four years. He introduced the Micro Lab protocol for use in group discussions. I have tried this with a Year 10 class and a Year 12 class and been impressed with the way students have responded and how it has improved their approaches to problem solving in mathematics. It involves:

•Dividing the class into groups of 3

•Each member decides which problem (out of 3 similar-themed ones) to start on (a different one per member)

•10 mins of individual time for students to work on their problem

•2 mins then for Problem 1 member to talk about how they went about their problem + 1 min quiet reflection following this presentation

•2 mins for Problem 2 person to do the above etc

•10 mins for group to come up with a consensus on all three problems

•Discuss these on the board with the class as a whole

I tried providing the same ‘stimulus’ material for all members of the group in one class (ie they all got the same problem to talk about) but this didn’t work as well as having three problems to discuss, each member having their own problem first of all. This protocol compels all students to talk about their thinking (not just the vocal ones) without interruption and allows for reflection. I found that students notice more things about the problems after they have had the opportunity to listen to someone else’s approach. During reflection time, I encourage students to note any questions they would like to ask, whether or not they agreed with the presenter’s approach to the problem and how this might compare with how they would approach that problem. In group discussion, students were more focused and had a way ‘in’ for each problem. No-one was completely stuck without a starting point. One of my Y12 students commented on how much she enjoyed the group work lesson as she felt more confident in her grasp of the mathematics, that it compelled her to engage more so than a ‘regular’ class. I was also pleased to note that her risk-taking capacity in lessons after this one increased. She was more willing to ‘have a go’, even if she wasn’t sure of her method or the correctness of her answer.

The approaches described above deliberately reflect and encourage noticing of the internal structures of mathematics and promote mathematical thinking (in both students AND their teachers!). They offer practical ways in which the culture of transmission that operates in many mathematics classrooms can become closer to a culture of thinking.

One of the problems that I used with the Year 10 class involved thinking about whether certain geometrical objects were possible or not. This is given below.

Look at each diagram and decide whether it is geometrically possible or not.

Think about how you decided on your response.

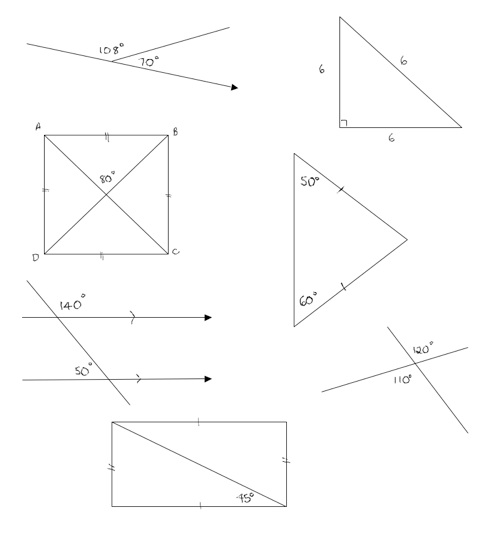
Again, the objects were purposefully chosen to address common misconceptions that students have about two dimensional geometry. Do the diagonals of a rectangle bisect the corner angles? Many students believe that a rectangle’s diagonal splits the corner angles into two halves, springing from the misconception that dividing into two always means dividing in half. By examining the diagram given (the last one on the sheet), I was hoping that students could see that the angle formed couldn’t possibly be 45 degrees. In the triangle formed at the bottom of the figure, as the corner angle is 90 degrees, the other angle in the triangle would also have to be 45 to make the 180 degrees of a triangle. But...this means the triangle has to be isosceles (two angles the same size) ...which it can’t be as the symbols on the rectangle show the two sides have to be different lengths...hence the premise that the angle made by the diagonal is 45 must be wrong. It wasn’t about ‘telling’ students the properties of a rectangle, it was about students discovering these properties for themselves. I believe that it makes for stronger connections in their brains and thus better, deeper, understanding.

Can a triangle with a right angle have all three sides equal in length? Look at the second diagram on the sheet. How would you start on this one?

Again, it was important to draw out these misconceptions, discuss them fully and correct them before students left the class so that the correct pathways were formed in their neural frameworks. It became a matter of drilling down into their conceptual frameworks to identify any cracks or gaps or incorrect connections; then trying to ‘shake these up’ using questions that created cognitive dissonance to make the brain wake up and pay attention; then reformulating these connections correctly.

At a conference I attended in 2009, Andrew Fuller recommended the following strategies, based on his knowledge of brain behaviour in adolescents:

•High level of feedback

•Repetition

•Ample time for wondering, being intrigued

•Opportunities for challenge, experiencing difference

•Making meaning

And his advice on the implications for teachers of mathematics? Mini review quizzes at the start of every lesson, more physicality in activities, more opportunities for student discourse and interaction, more problem solving. To expand students’ memory capacity, he advised increased repetition of key ideas and processes, the use of new information deliberately to link into already-held knowledge and describing things in different ways.

As I have previously mentioned, I can no longer justify separating classroom experiences into ‘problem solving’ and ‘skills’. I now believe it is possible, desirable - no; imperative! - to teach mathematics for understanding. Start with purpose and carefully consider what we want our students to be able to do (skills), understand, and know for every lesson in every topic, then deliberately align all learning activities to those learning objectives and assess for our students’ learning at regular intervals.

The Maths 300 lessons are great but sometimes go off on tangents that take students (and teachers!) away from the concept one is trying to instill. Here I agree with Andrew Fuller – adolescents need repetition of the ‘big idea’, they need to be focused on that big idea to develop understanding and create their own meaning. That’s the job of the teacher: to decide what the big idea is and design learning activities that deliberately address and continually re-inforce this big idea.

Take the Radioactivity Maths 300 activity. I use it as an introduction to exponential functions in Year 10. We start with 1/6 as the rate of decay, we do the die activity, we plot the class results as a graph. My objective is to develop the understanding that multiplying by the same constant for each successive value of the independent variable, always results in a similar curve that we call exponential decay (or growth), and that the magnitude of this constant determines the rate of decay, or growth, of these curves. Hence, my next step is to discuss the shape of the graph obtained. Why isn’t it linear? (Opportunity here to repeat the conditions that result in a linear graph) Why is it coming down? We talk about half life. We do it again with a different rate of decay. We stop and compare. What’s the same as before? What’s different? Why? What if we ‘grew’ rather than decayed? What if the number of atoms doubled each year?  I have a clear learning objective in mind; I keep bringing my students’ focus to that. I then transfer that understanding to some skills-based questions on exponential rules and graphing.

 

How is this different from a ‘typical’ lesson in mathematics? Skills seem to be done in isolation and prior to ‘using’ them. I start with ‘the whole game’ – as David Perkins would say – then draw out the understanding I wanted and use this as a justification for learning about the related skills. This is how I think mathematics is best taught. With understanding comes engagement. Students can ‘work like mathematicians’ every single lesson!

 

I am currently trying to put this into practice for each topic. I hadn’t seen the Maths 300 Soft Drink Cans activity prior to attending the conference at which Andrew Fuller spoke. It was recommended as a ‘strategy lesson’– to teach students about breaking a problem down into manageable chunks, considering one aspect at a time. For those who don’t know it, students are given a 6×4 rectangular grid and 18 cubes.

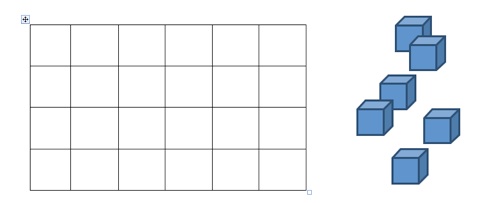
The problem is to place the cubes onto the grid in such a way that every column and every row has an even number of cubes in it.

This proves to be quite tricky, and frustration tolerance is tested. After about 5 to 10 minutes, the class is stopped and the teacher brings everyone around one student’s table. He/she asks the student to arrange the blocks on the grid so that every row has an even number of cubes, forgetting about the columns for the time being.

For example:

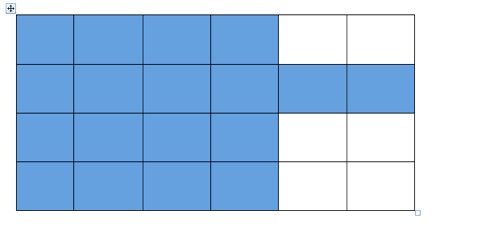
When this is done, the teacher says…”Now, slide cubes along the rows – but keeping the rows intact in total - to make the columns all contain an even number of cubes” The problem becomes incredibly easy with this simple instruction.

For example:

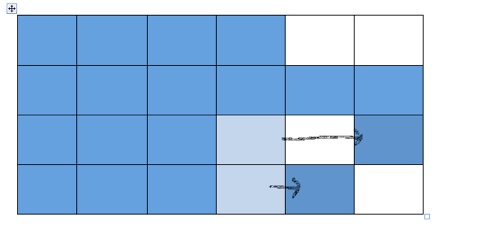
The Maths 300 lesson then extends the problem in various ways but this won’t help students transfer knowledge of this strategy into other situations; it just contains it to this situation, which is a ‘nice’ problem but unrelated to curriculum ‘content’.

I immediately thought of its application to solving simultaneous equations. The whole idea of solving simultaneous equations is to deal with one variable first then come back and find the other one. I planned to try this first then, in the same lesson, start simultaneous equations and try and embed the strategy in some skills work straight away so that students’ brains can make the connection and thus strengthen the procedural link.

It all went very well. We started with two simple equations as part of their daily quiz – to solve for a and b in a + b = 3 and b = a + 1 (ie something they could do relatively easily by trial and error). I then challenged them with 2a – 3b = -1 and a = b + 1. We briefly talked about needing a strategy for more complicated ones.

I then handed out the grids and blocks. The activity itself generated interest, engagement and a challenge. In a class of 22, I had three students who found one solution in 10 minutes and I asked them to try and find another whilst walking around the room and checking on what the rest of the class was doing. I wouldn’t keep it going for any longer than 10 minutes. We then all went to the desk of a student who hadn’t found a solution as yet and I asked her to fill in the rows with an even number of blocks and not worry about the columns as yet. She was a trifle daunted by the prospect of doing this in front of everyone but, although I don’t think she enjoyed the ‘exposure’, I think it pushed her thinking and learning behaviours in positive ways. She needed some assistance to then finish the problem but the majority of students ‘got it’ and they went back to their own problems to get at least one solution.

I then asked about a possible connection between the activity they just did and the two equations. Quite a few of the students were excited to realise the connection. We discussed how we could obtain the value of one variable then find the other. I showed them the substitution method. I kept repeating the main idea – that to solve two equations with two unknowns by hand, we had to keep using the strategy of finding one variable first then thinking about calculating the value of the other.

In subsequent lessons, we talked about pairs of equations that didn’t have a ‘letter on its own’ and what we could do, but I made sure to always come back to the strategy – how can we solve for one pronumeral first? I was very pleased with both the way the activity added to their understanding that the two algebraic methods of solution were just different forms of the same strategy, and the way in which it engaged and made all feel as if they were in control of what they were learning – not just copying down a procedure that someone else had thought about.

In classes, do students ask questions that focus on procedural things or questions that relate to the learning? Is there real interplay in the discussions in classrooms? That is, not ‘just’ student question-teacher response; teacher question-student response but student-student discourse that is spontaneously generated and isn’t filtered through the teacher.

One of my greatest joys in the classroom comes when a student is doing a problem on the board and others start commenting on what this student is doing or has done….commenting, not to me, but directly to the student. I sit at the back of the room and lap it up. “How did you get that answer?” “I got it by doing x, y and z”  ”Why did you do y first and then x?”  “Can anyone help me out here? I don’t know what to do now” Sure, there are still moments when these are directed my way but I am doing my utmost to encourage real dialogue between my students, real ‘argument’ (in a Socratic, academic way), real application of mathematical thinking.

This discussion helps me too. It gives me information about their thinking that informs my future instruction. When students have ‘completed’ their problems, I give them the opportunity to think about it and change their responses if they want to. I emphasise the importance of being able to make mistakes and learn from them. As Ron Ritchhart has said, teachers have the dominant voice in classrooms and it’s important we are continually open to think of ways in which we can increase the student voice…to increase the level of ‘tentative talk’ as students think and wonder and engage with the ideas in order to develop their own conceptual frameworks.

A number of researchers have commented on the importance of feedback in effective learning. Most notably, the work of John Hattie tells us that feedback is one of the prime factors affecting quality learning. Feedback should

•Cause thinking

•Provide guidance on how to improve

•Focus on what to take forward to the next assignment rather that what is deficient about the last assignment

•Be used

So, at the same time that I was endeavouring to promote and provoke mathematical thinking by the types of questions and learning activities I was using, I was also mindful of focusing students’ attention on the big ideas that support and frame the discipline, while ensuring that the timing, quantity, frequency and type of feedback informed and improved their learning. What did this look like?

In my Y10 and Y12 classes, I have been trying to ascertain prior knowledge through pre-tests at the start of topics; adopting formative assessment approaches and 'check for understanding' quizzes to track students' learning throughout the unit; and using the responses on these quizzes to give students feedback on their thinking and, concomitantly, re-direct my instruction in classes to try and deliberately address errors in thinking. I then give a 'follow up' activity after the formal end-of-topic test that addresses mistakes made. In these activities I have tried to focus attention on why they made certain errors, not just ‘more of the same’.

For example: Highlight the questions you got wrong in the following table and briefly write down what you did that made it wrong.

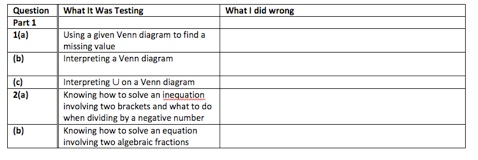
Why did you make these mistakes? Tick the box that best describes what you did.

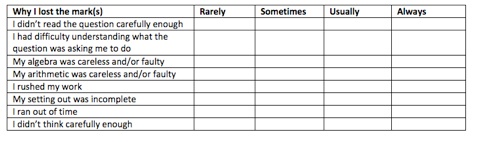
My intention is to emphasise the ongoing journey of learning and how it doesn't stop at the test. Mistakes are used to focus future learning. I have 'ditched' the revision class before the test in favour of a follow up after the test class, where students work in groups to assess the learning shown on the test. I have increased the frequency of written quizzes (which I call Check for Understanding quizzes) which students complete at the start of a topic (to act like a pre-test) and during the topic so that, hopefully, students don’t get ‘lost’ so often and I am given more authentic opportunities to intervene and re-direct.

My most recent light bulb moment involved how I view feedback. It’s the feedback that students provide me, rather than what I provide them, that yields the most valuable information as to how I am performing as an educator. This is gained through the questions they ask and how they go about their mathematical learning and their mathematics, reflected in their written work.

And so I ask myself:

•Do the assessment for learning approaches make a difference to embedding 'good' brain pathways?

•Do the check for understanding quizzes pick up the 'bad' thinking pathways and change them for the better? Is the feedback students receive from them effective?

•Do I see the same mistakes being made time and time again in every activity and in the test and follow up? If so, why?

What has become clear is that the feedback must be immediate to prevent the wrong connections forming in students’ brains. The Check for Understanding quizzes have been a wonderful adjunct to my instructional repertoire. I give them out at the start of a lesson and, whilst students work on a set of problems in groups, I correct them and call students individually to discuss errors in thinking detected. I have deliberately used questions from last year’s tests so that students know the standard of questions they will be asked and to form a continual review throughout the topic. In their reflections at the end of term, students have commented favourably on these quizzes and say how much they have helped them address conceptual difficulties before the test (the formal assessment that ‘counts’ for them as it goes on their semester report) rather than after it.

My feeling is that these checks must be written and must be done by all. In the past, I used a quiz on the board as my lesson starter (and still do). I use this quiz to review past material, extend thinking via problems that use the same content in different ways and then challenge them with questions that lead into the lesson’s focus for that day. This has served me well and past students always say how much these quizzes helped them get a handle on their understanding. But it allows some students to opt out. I deliberately choose students to come to the board to explain their thinking who don’t volunteer to show their approach to the class but this isn’t enough. There are always some other students who wait to see what someone else does and who never actually engage their thinking drive. The only way to ensure that no student can opt out is to require all to do a written quiz and submit it.

I am disappointed to have seen the same errors being made time and time again by certain students- usually the ones who resist most strongly learning for understanding. They are frequently the template learners, the ones who want to follow a pattern; the ones who don’t take many risks, who don’t like mistakes, who perhaps don’t believe that mistakes are a necessary part of learning. Sometimes they are the ones who have achieved good results in the past due to diligent memorisation and repetition, but have little real understanding of the mathematics. The ones who think learning is something I do for them and to them.

The ones I need to work on.

This is my next quest. To try and work out a way I can positively address these affective behaviours, so common in mathematics classes, which result in these students lacking resilience, lacking the drive to change their approach and move forward.

In general though, as a result of my focus on trying to make my classroom a culture of thinking, my teaching and classrooms have changed.

How?

•The biggest change has been the creation of 'check for understanding' quizzes throughout topics and assessment for learning activities that deliberately try and address misconceptions before they become 'concrete'

•A focus on big ideas in mathematics and in the topic being studied

•Continual, purposeful review

•The modelling of 'acting like a mathematician' for students and pointing out to them what I'm doing eg. linking to prior knowledge, looking at a simpler case

•Trying to become less 'sage on stage' and more student-student discussion happening so that students don't always look to me for an 'answer'

•A focus on questions and prompts that provoke and promote thinking, rather than a focus on ‘right’ answers

•A focus on justifying a position and the expectation that reasoning is required to support a position

As I've worked with these ideas, I think that the kinds of shifts and changes that are occurring in students as thinkers and learners are:

•Students expect to both know and give a 'why'

•Students expect to see criteria in assessment

•Students are happier to ask each other, not always me

•Number of procedural questions has reduced

•Students are using 'thinking language' in their reflections and acknowledging that their teacher makes them think (I use the statements given in the appendix in each reflection)

•Students are more comfortable taking risks as they realise mistakes are a necessary part of learning

•Students are more interested in knowing how to learn better, not just how to get a better mark

It isn’t over yet. It will never be over. The journey that is my learning, about my teaching and my students’ learning, ‘works in me like madness’

“And there’s no end of voyaging when once the voice is heard”

Appendix

Reflecting on the term:

Respond to the following by putting a tick on the line where you best think your response lies.

12345

    not at all true   somewhat true       very true

My teacher makes sure that the work I do really makes me think.

12345

My teacher presses me to think deeply and go beyond just finding the answers

12345

My teacher asks me to explain and give reasons for what I think

12345

My teacher thinks mistakes are OK as long as we’re learning

12345

My teacher wants us to understand our work, not just memorise it

12345

My teacher gives us time to really explore and understand new ideas

12345

My teacher encourages us to build on and extend others’ ideas

12345

I’m confident that I can have a go at the most difficult and challenging problems

12345

We are encouraged to discuss ideas with each other in this class

12345